什么是拐点模型？
拐点模型的核心是一组平行线与一个点，然后把点与两条线分别连起来，就构成了拐点模型，这个点叫做拐点，两条线的夹角叫做拐角。
1、点在平行线中间
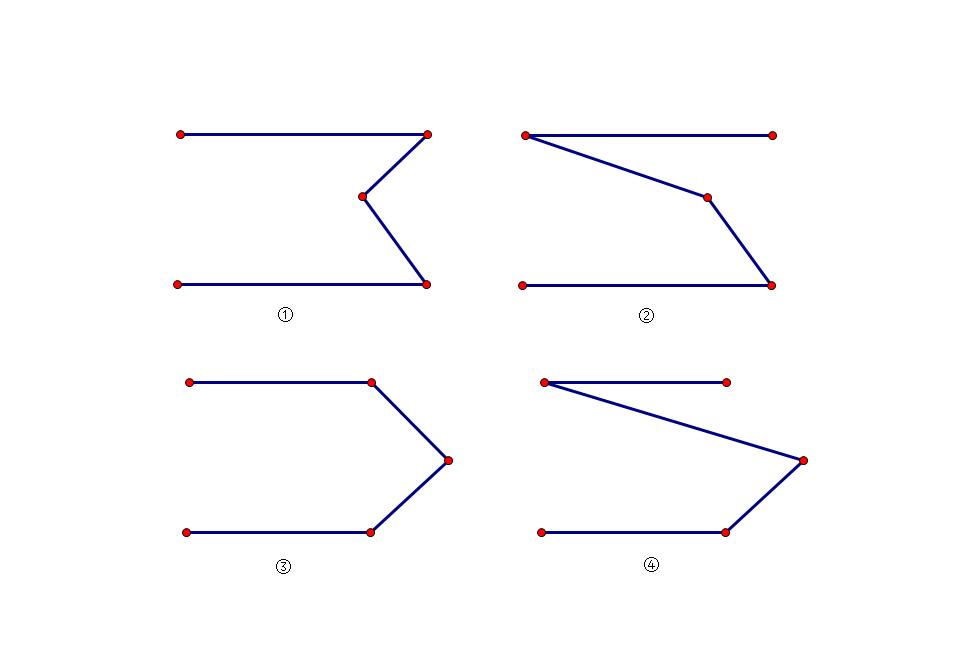
2、点在平行线外
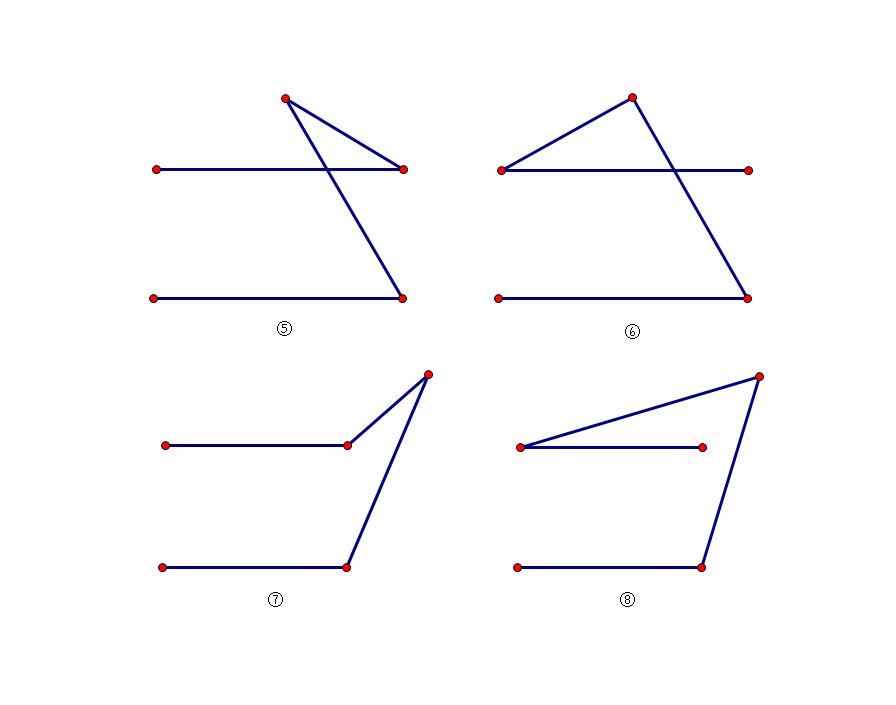
最常见的拐点模型是①③⑤⑦，尤其①③更是常见，分别叫做猪蹄模型和铅笔模型。
三、拐点模型的通用解法与基本思路
通用解法：过拐点作平行线，基本思路：和差拆分与等角转化。
1、和差拆分：过拐点作平行线后，拐角就可以用角的和差来表示。如果平行线在角的内部，则拐角可表示为两个角的和；如果平行线在角的外部，则拐角可表示为两个角的差。
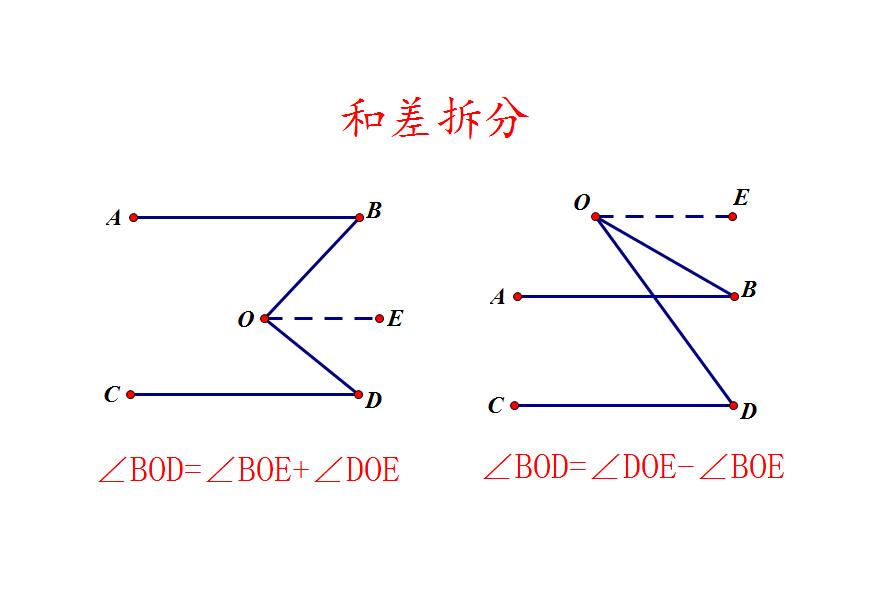
2、等角转化：平行线模型都具有等角转化功能，可用同位角、内错角或同旁内角来等量表示。
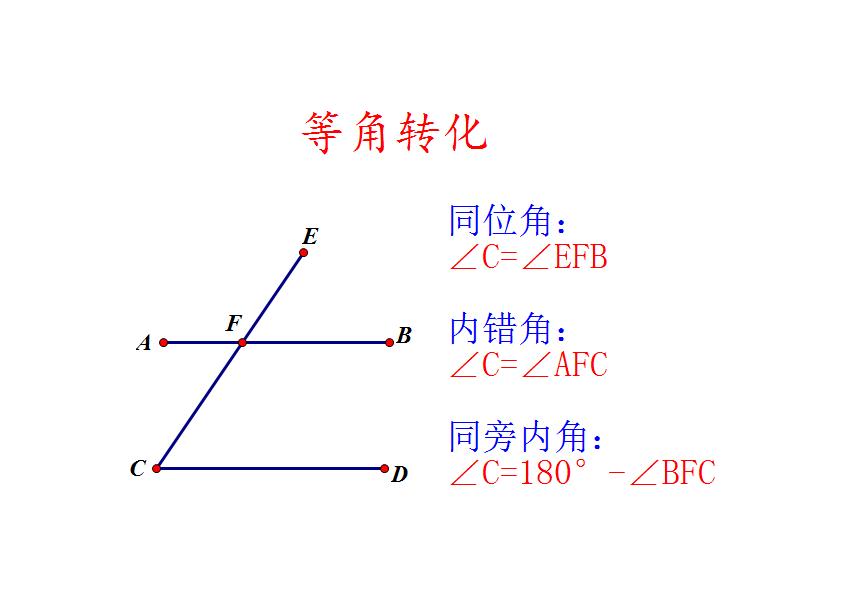
四、例题
下面以模型②⑥为例，具体解释一下。
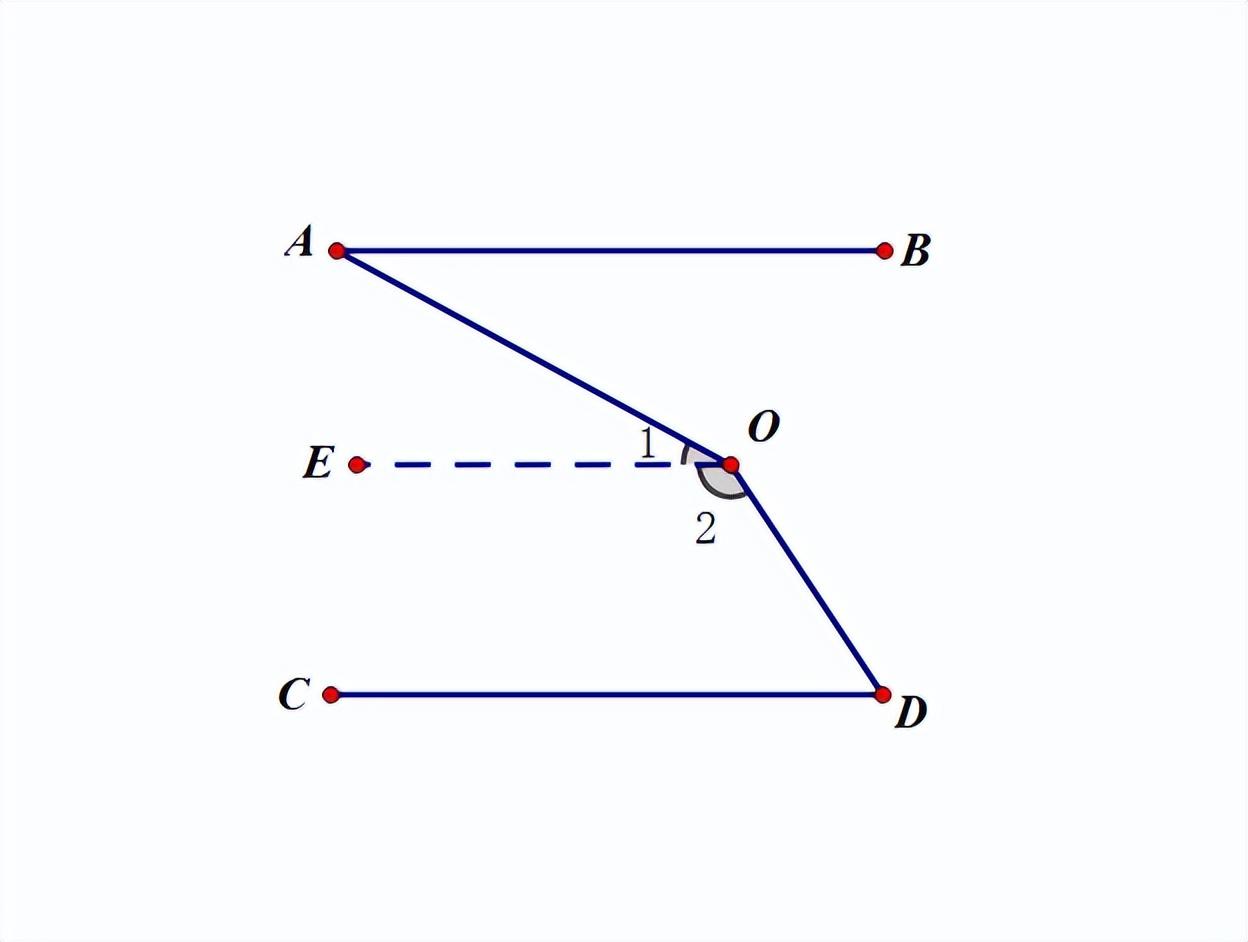
例1、如图，AB//CD，试猜测∠AOD与∠A和∠D的关系并证明。
分析：如图，首先过拐点作平行线OE，则∠AOD可通过和差拆分转化为角的和∠1+∠2，然后利用平行线的等角转化，∠1表示为∠A，∠2表示为180°-∠D，∴∠AOD=∠A+180°-∠D
解答：
∠AOD=∠A-∠D+180°，理由如下：
过点O作OE//AB
∵OE//AB（辅助线做法）
∴∠1=∠A（两直线平行，内错角相等）
∵OE//AB（辅助线做法），AB//CD（已知）
∴OE//CD（平行于同一直线的两条直线互相平行）
∴∠2=180°-∠D（两直线平行，同旁内角互补）
∴∠AOD=∠1+∠2=∠A-∠D+180°（等量代换）
例2、如图，AB//CD，试猜测∠AOD与∠A和∠D的关系并证明。
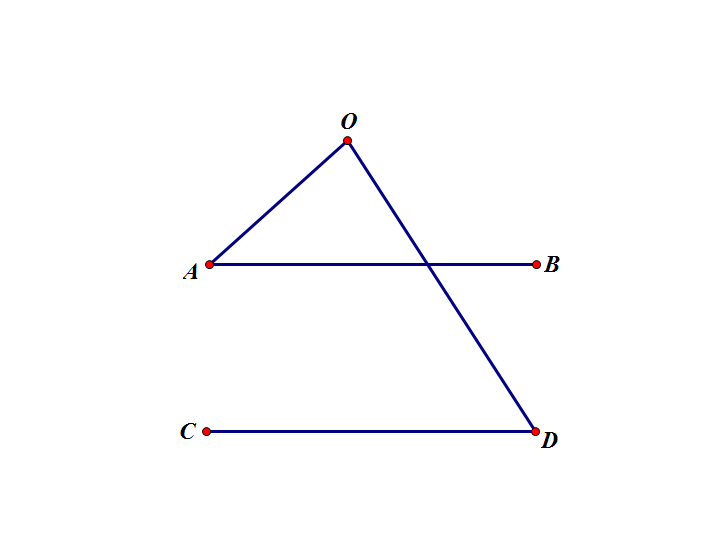
分析：同例1类似，首先过拐点作平行线OE，所不同的是，因为本题辅助线在∠AOD的外部，所以和差拆分转化为了角的差∠EOA-∠EOD，然后再利用平行线的等角转化，∠EOA转化为180°-∠A，∠EOD转化为∠D，∴∠AOD=180°-∠A-∠D.
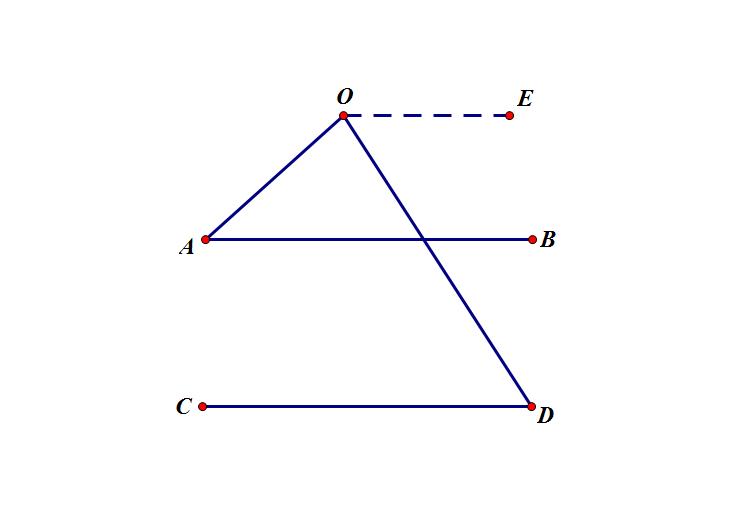
解答：
∠AOD=180°-∠A-∠D，理由如下：
过点O作OE//AB
∵OE//AB（辅助线做法）
∴∠EOA=180°-∠A（两直线平行，同旁内角互补）
∵AB//CD（已知），OE//AB（辅助线做法）
∴OE//CD（平行于同一直线的两条直线互相平行）.
∴∠EOD=∠D（两直线平行，内错角相等）
∴∠AOD=∠EOA-∠EOD=180°-∠A-∠D（等量代换）
五、小结
1、练好基本功，贪多嚼不烂
一题多解的确可以培养学生的发散思维，但前提是基础要牢，应首先掌握常用方法的多解归一，否则即使方法再多，也不过是花拳绣腿、空中楼阁。事实上，中考阅卷中发现，有很大比例的学生证明题过程都是乱写的，即使是简单题，就像某位同事所说“不要把他们想的太聪明，差得远呢！”
2、书写要规范，证明过程要有理有据
拐点问题学生出错很多，有辅助线描述乱写的，有直接利用拐点结论的，有由OE//AB直接得到OE//CD的，胡乱省略、跳步，证明过程上下不存在因果关系等等。
3、教师应多从学生角度考虑问题
对于普通学校的绝大部分学生，学生学习能力其实是极其有限的，不能把他们想的太高。
相关文章：
歧义什么意思（什么是词汇歧义）11-01
货车载重标准对照表（半挂车载荷吨位标准是怎么算的？）11-01
面试怎么自我介绍更突出（如何在自我介绍中展示您的实力和能力？）11-01
萧关古道可以指庆阳（庆阳石道坡：黄土高坡上的丝路古道）11-01