在数学世界中，深刻理解最基础概念对于探索更深层次的知识至关重要。
公因数(Common Divisor)这一概念，虽看似简单，却在数学的许多领域扮演着重要的角色。它是指能够同时整除两个或多个整数的数。无论是更深入数论的领域，还是执行日常简化表达式的操作，掌握公因数都是必要的。
例如，让我们考虑两个数：140 和 110。它们的因数列举如下：
- 140 的因数有：1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140
- 110 的因数有：1, 2, 5, 10, 11, 22, 55, 110
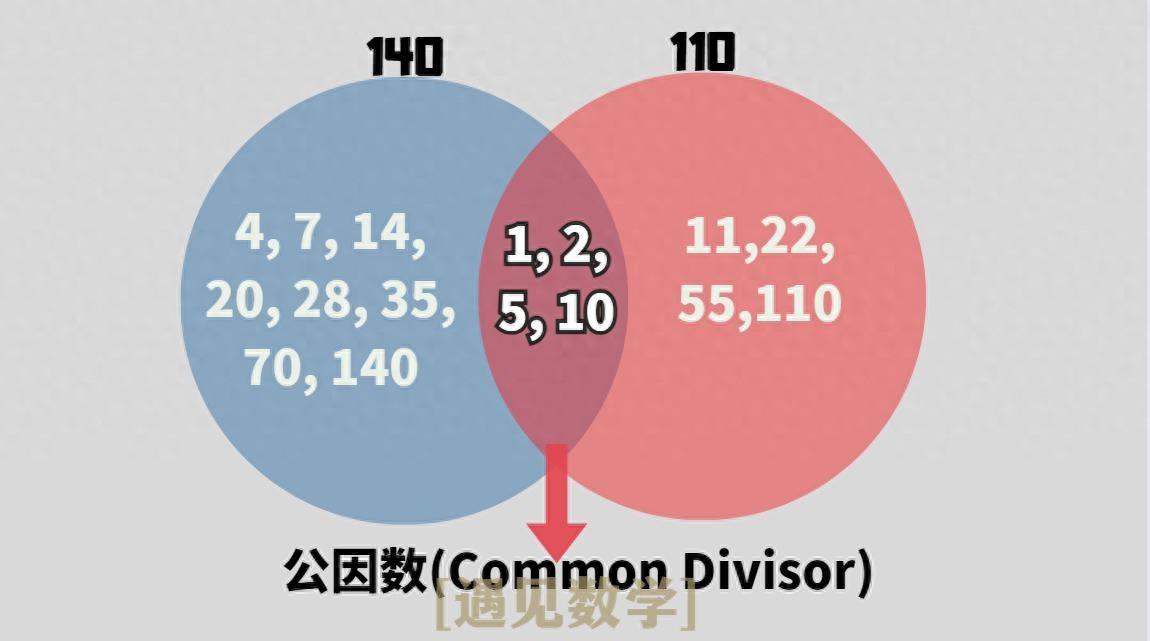
比较这两组因数，马上就能发现 140 和 110 的公因数——即 1, 2, 5 和 10。这意味着这些数可以同时整除140和110。
这一概念可以形式化地表述为：
若 d 是两个整数 a 与 b 的公因数，那么存在整数 a₁ 和 b₁，使得 a=d * a₁ 与 b=d * b₁。
公因数的一个性质
公因数 d 的一个非常有趣的性质是它不仅可以整除 a 和 b，而且也能整除它们的和 a+b 和差 a-b，这可以用下面的等式展示：
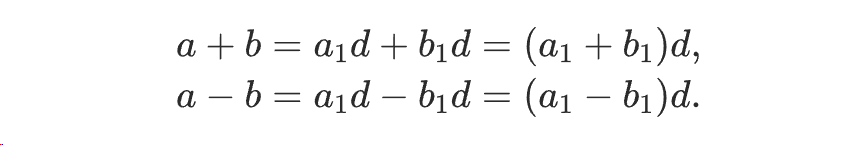
如果知道了 d 是 a 和 b 的公因数，那么也就知道 d 必是 a+b 和 a-b 的公因，这在解决涉及整数和它们之间关系的问题时会有用。
最大公因数
最大公因数（Greatest Common Divisor，gcd）是指两个或多个整数共有约数中最大的一个。对于任意两个整数，其最大公因数是能够同时整除它们的最大正整数。了解最大公因数对于简化分数和解决与整数有关的各种数学问题非常有帮助。
最大公因数通常用符号 gcd 表示，例如 gcd(140, 110) = 10。
如何找到最大公因数
求最大公因数有几种常用的方法，每种方法都有其适用的场景。本文介绍素因数分解的方法。
例如，对于 a = 980 和 b = 770，如何找到它们的最大公因数 d₀。首先，我们将两个数分别分解成素因数的形式：
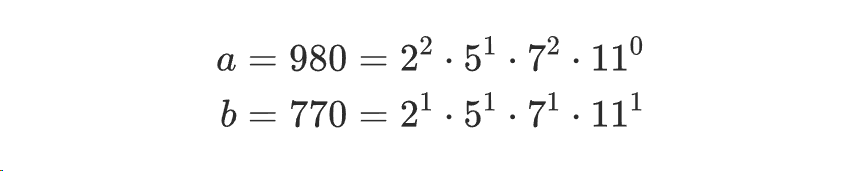
在寻找最大公因数时，我们比较相同素因数的指数，并选取最小的指数：
由于素因数 11 只在 770 中出现，它不是两个数的公因数。我们将这些素因数的最小指数相乘，算出了最大公因数 d₀：
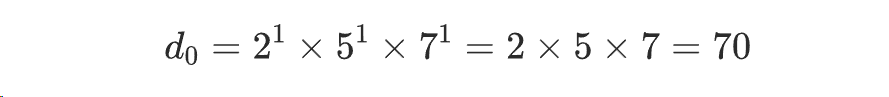
最大公因数的一个性质
在我们找到最大公因数后，还能得到下面这个性质：
任一公因数 d 一定整除最大公因数 d₀。
就是说，最大公因数 d₀ 的所有因子都是两个数的公因数。这是因为，最大公因数 d₀ 由两个数共有的素因数按其最小指数构成，所以 d₀ 的任何因子都由这些公因数中的某些组合而成，且指数不会超过最大公因数中的指数。
这也是为什么在数论和算术中，寻找最大公因数是非常有用的，因为一旦找到了最大公因数，我们就能立即知道所有的公因数。
利用素因数分解求最大公因数的方法在处理较大的整数时可能会非常繁琐。一个更有效的方法是使用辗转相除法（也称为欧几里得算法）来计算两个或更多整数的最大公因数。
相关文章：
歧义什么意思（什么是词汇歧义）11-01
货车载重标准对照表（半挂车载荷吨位标准是怎么算的？）11-01
面试怎么自我介绍更突出（如何在自我介绍中展示您的实力和能力？）11-01
萧关古道可以指庆阳（庆阳石道坡：黄土高坡上的丝路古道）11-01